How we are writing modern Javascript with AngularJs
Preface Writing slick user interfaces has never been so delightful as it is now. You’ve got amazing frameworks, state management patterns…
Computing Aggregates in VWO
Introduction In VWO, we present clients with information about the data of their users' events in aggregated form on their dashboard…
Google BigQuery: Why & How we power our Data Platform with it
Introduction BigQuery is a completely serverless and cost-effective enterprise data warehouse provided by the Google Cloud Platform. Just…
Network Mocking in Playwright
The Requirement In VWO, we have our client-side library which is executed on our customer’s website and it is the stepping stone of every…
Why functional programming is needed
A Little History Having a functional approach to a problem does not kick off the adventurous journey of learning a new language, instead, it…
Automating Tedious Managerial Tasks
Client issue assignment and tracking. We at Wingify take our client issues very seriously and have built processes to get the desired…
Rest Assured - Journey to the end to end API automation
REST Assured is a Java-based library, one of the most popular libraries to test RESTful Web Services, and is used to perform testing and…
Playwright – The Rightful Heir
The hunt has ended. Protractor's successor has finally been found! Introducing Playwright, the new star of test automation:-). An end-to-end…
The Big Bug Hunt - Wingify
Quality is never an accident. It is always the result of intelligent effort. In line with the above quote, we organized a quality-focused…
Cypress - A worthy replacement for Protractor?
We, at Wingify, have implemented our web automation tests using Protractor. Although the old horse has served us well it is fast approaching…
Kroomsa: A search engine for the curious
Introduction The search algorithm implemented in your website greatly influences visitor engagement. A decent implementation of a search…
Finding Bughotspots in Source Code
Introduction We are often faced with the problem of source code that breaks frequently. Or those modules which are very sensitive to changes…
Handling Shadow DOM in Protractor Tests
Overview Shadow DOM has slowly and steadily become an integral part of modern web apps. Before this, the Web platform provided only one way…
Designers should understand code
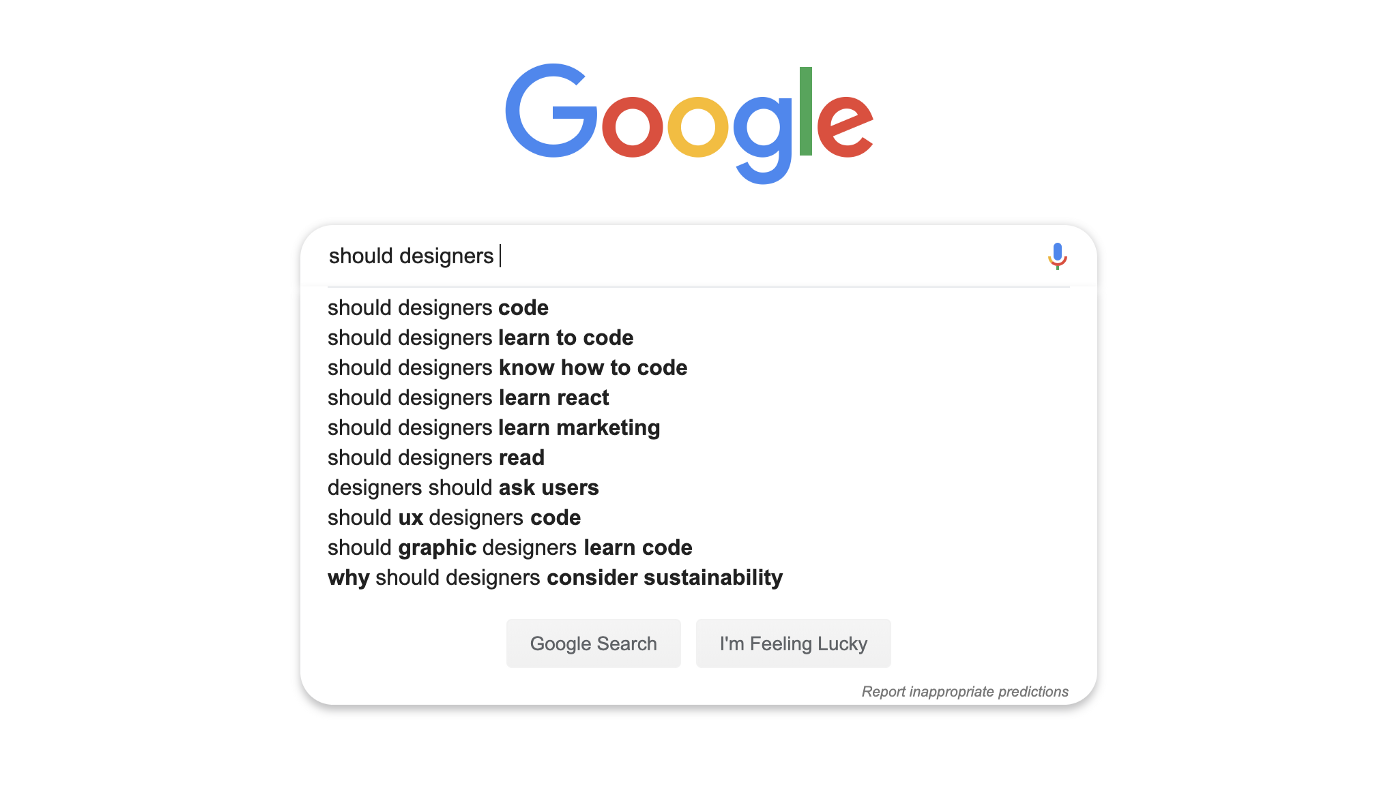
The term designer is used across many domains. In the context of this article, it refers to a UX (User Experience) designer. One question…
Wingify CTF 2k21
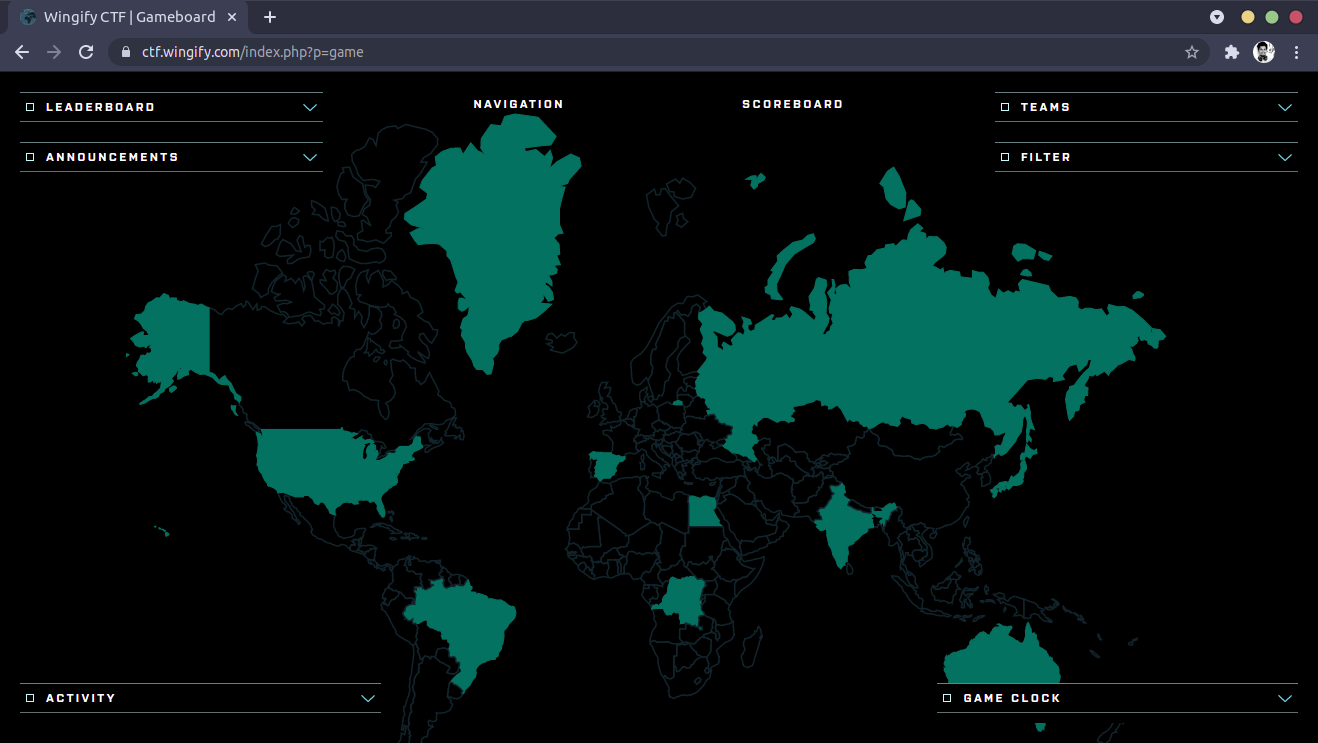
Here at Wingify, we love solving problems and puzzles. To spread this spirit of problem solving, we organized the fourth edition of Capture…
Performance Testing a data pipeline at scale
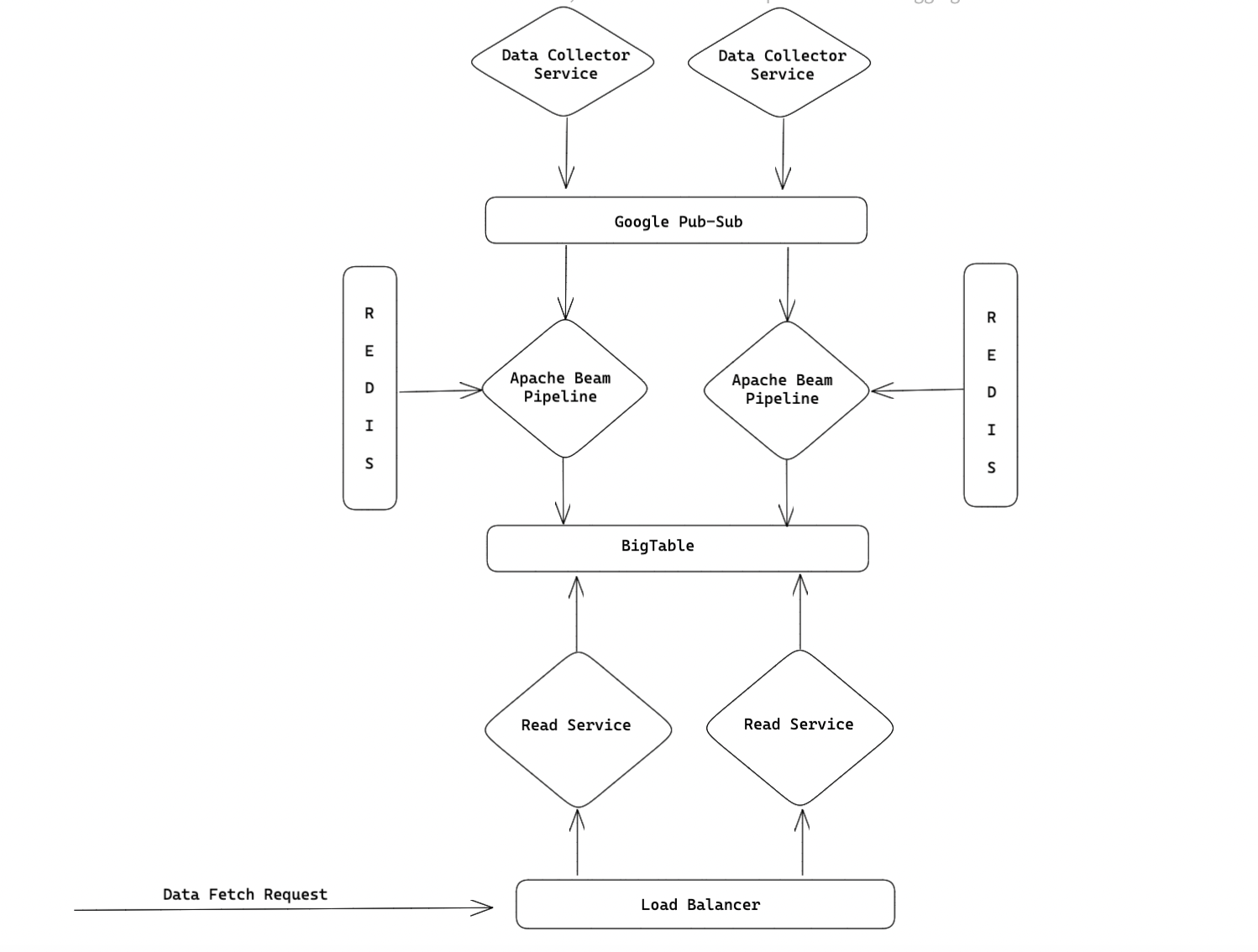
Introduction At VWO, we get traffic at a very high throughput (22K req/sec) to our servers. The data pipeline crunches and transforms the…
Maths behind Bayesian Duration Calculator
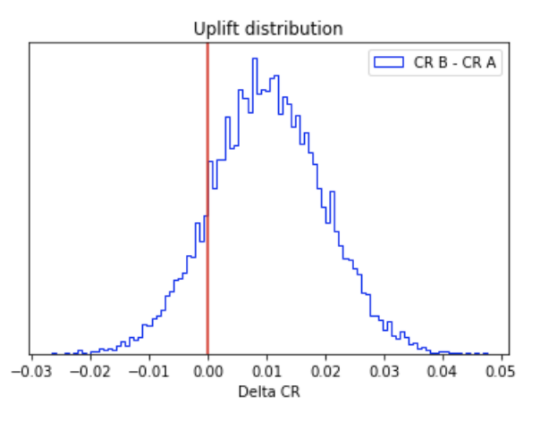
Introduction The culture of experimentation is strongly picking up in several sectors of industry. It has become imperative to measure the…
A lua-nginx Client for Pub/Sub
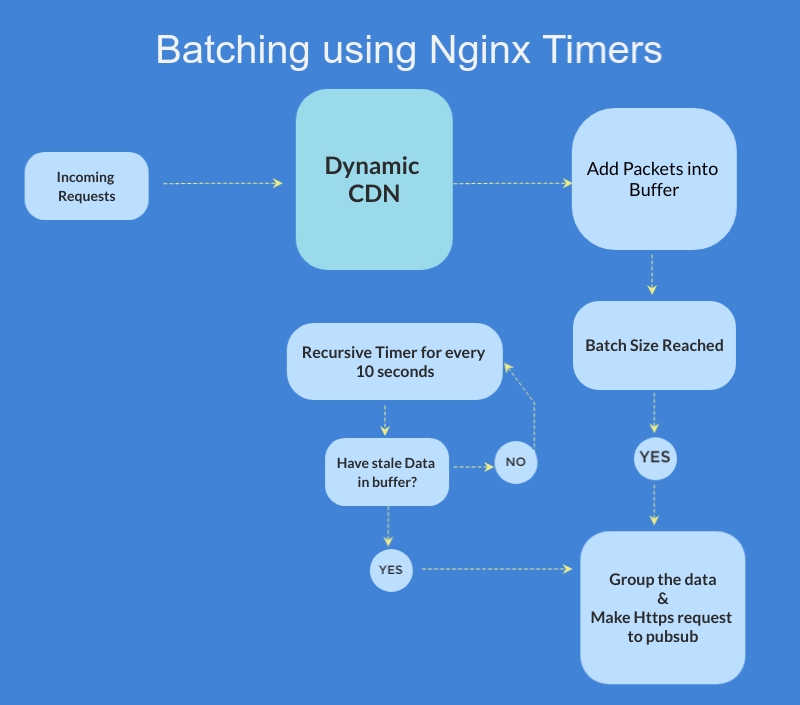
Introduction Lua as a part of the OpenResty package, is extensively used in our in-house Dynamic CDN (DACDN) module. CDN generally is used…
Kafka Streams Stateful Ingestion with Processor API
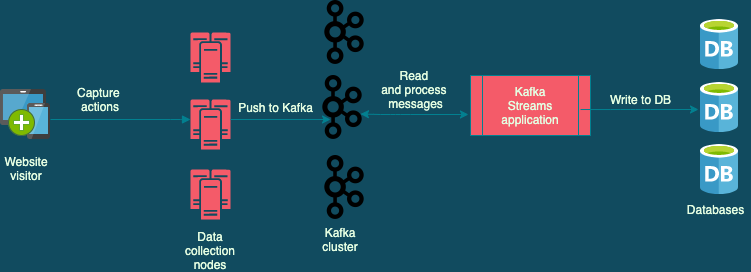
At Wingify, we have used Kafka across teams and projects, solving a vast array of use cases. So, when we had to implement the VWO Session…
Programmatic Authentication under IAP on GCP
Overview We recently started with moving a lot of our infrastructure onto Google Cloud Platform. With this, we also decided that a lot of…
Performance improvements in VWO SmartCode
VWO puts a lot of focus on ensuring websites remain performant enough while using VWO. We have been increasing the efforts in this area and…
Three Wingifighters at the BountyCon
On March 29th, 2019, our team members Ankit Jain, Dheeraj Joshi and I had the privilege to attend a very exclusive event called BountyCon in…
Wingify towards Docker and Kubernetes
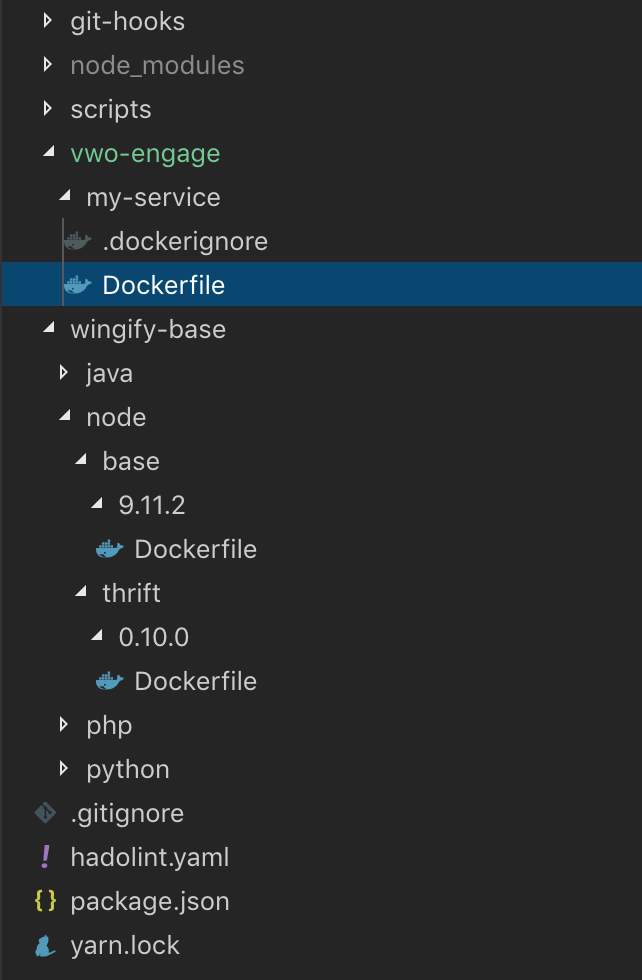
Introduction: At Wingify, we follow microservices based architecture to leverage it's great scalability benefits. We have a lot of…
JS13K Games 2K18
Introduction: Js13kGames is a JavaScript game development competition that is organized every year from 13th August to 13th September. What…
Shift to Atomic CSS
For the past few months, we at Wingify, have been working on making a common platform for different products - so that things get reused…
Demystifying Webpack 4 Split Chunks Plugin
Recently, we migrated one of our web apps to the Webpack 4, which decreases build time and reduces chunk size by using Split Chunks plugin…
Automated Heatmap Verification E2E using Selenium and Canvas
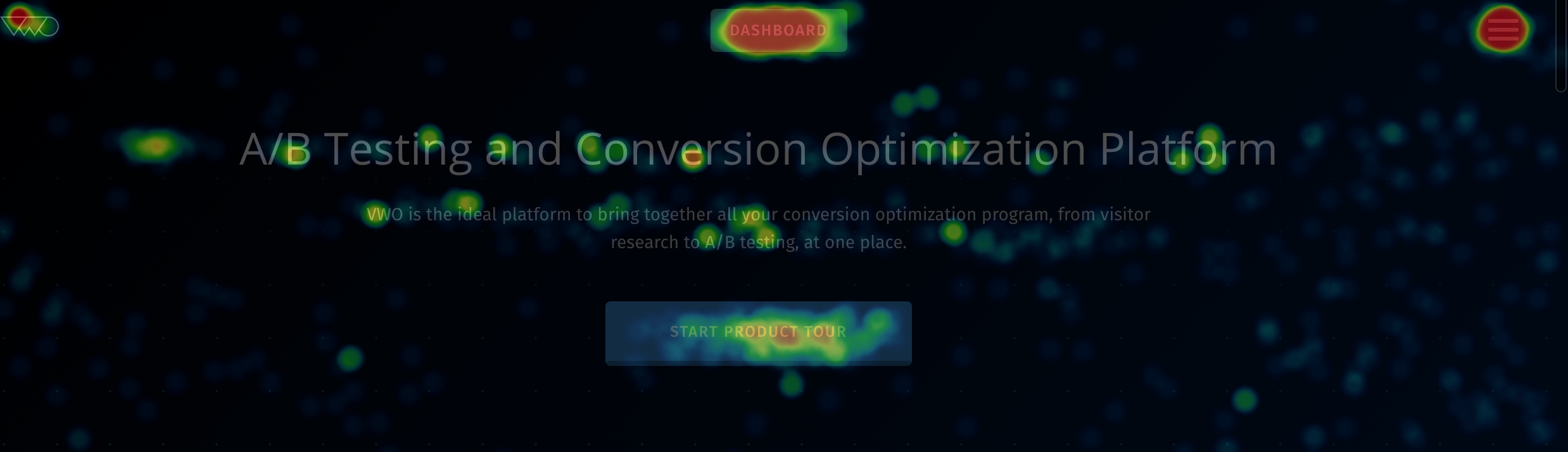
Heatmaps record visitor clicks on the live state of your website, which can be used to interpret user behavior on elements like modal boxes…
Animations in VueJS
This article is inspired from Animating Vue JS by Sarah Drasner at JS Channel 2017. Problem Statement - Why Animation? Website UI…
Why we've removed Inheritance/Extend from SASS & you should do the same!
SASS is a preprocessor that provides features like variables, nesting, mixins, inheritance and other nifty goodies and makes CSS clean and…
Leveraging Kafka Streams to reduce DB Hits
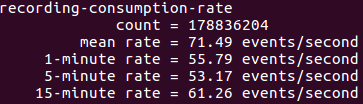
I have been working with Apache Kafka for more than 4 years now and have seen it evolve from a basic distributed commit log service…
Migrating towards Yarn and Webpack
For the past couple of years, we have been using require.js for module loading and Grunt for automating tasks on front-end, for one out of…
The First Wingify DevFest
"What is the most resilient parasite? Bacteria? A virus? An intestinal worm? An idea. Resilient... highly contagious. Once an idea has taken…
Automated environment deployments
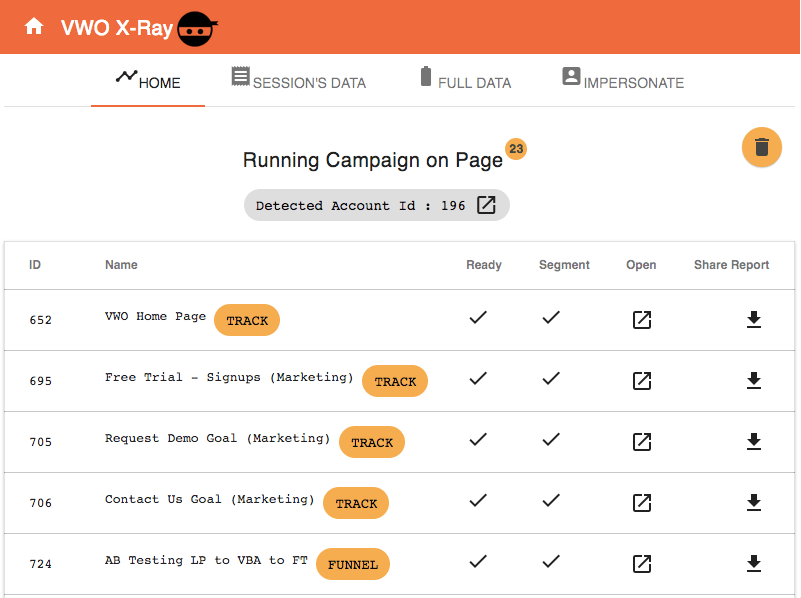
Shipping a bug-free feature is always important in every release. To ensure this, we do quality analysis(QA) at various points of the…
PyData at Wingify - My Experience
About PyData I recently got an opportunity to speak at the PyData, Delhi. PyData is a tech group, with chapters in New Delhi and other…
Demand-driven APIs Using GraphQL
Introduction This article will deal with the issues we face with the current API architecture (mostly REST) and why demand-driven APIs seem…
Wingify's First Internal CTF
Capture the Flag (CTF) is a special kind of information security competition which provides a safe and legal way to try your hand at hacking…
Wingify Hackathon - Sum It Up
I am a frontend developer at Wingify and I am building a really awesome product, PushCrew. Last month, we had a hackathon. The idea was to…
Wingify Hackathon - VWO X-Ray
Recently, Wingify had organised a 24-hour Internal Hackathon where the developers from Wingify created a lot of awesome projects for daily…
Wingify at Europe/UK Conferences
Last two months were quite amazing for me as a Wingifighter; I was on a traveling spree over Italy and London. I got an opportunity to…
Heybot! - Our skype bot
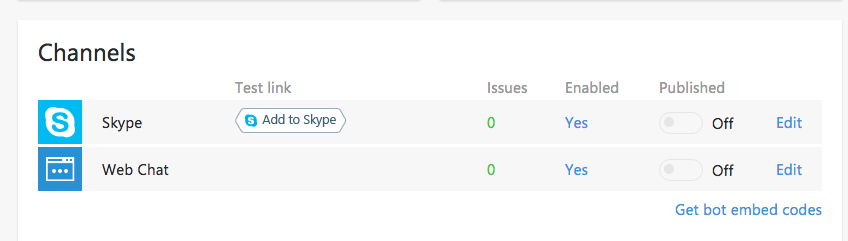
Few days back, we open-sourced our internal Skype bot to the world. Its called Heybot!, but we call it Ramukaka at Wingify :) Whether its…
Speeding Up VWO
About two years ago, Wingify had introduced the new generation of our Visual Website Optimizer to the world. Boasting a modern visual…
Secure Your Web Application @JSChannel Conference ’16
Recently, I spoke about securing Web Applications at JSChannel Conference ’16. The conference venue was The Ritz-Carlton, Bangalore…
Automating Web Push Notifications @Selenium Conference 2016
There were just two hours left to catch a flight for an exciting opportunity to present at the biggest Selenium conference, SeleniumConf…
Let's talk Security - Engineering Talkies
At Wingify, we recently began an initiative by the name Engineering Talkies where our engineering teams share their experiences, repertoire…
Code In the Dark at Wingify
Coding is always fun at Wingify, be it a Wingify Camp or a Fun Friday. And to add to the fun, in a Fun Friday Code In the Dark was organized…
A layout trick
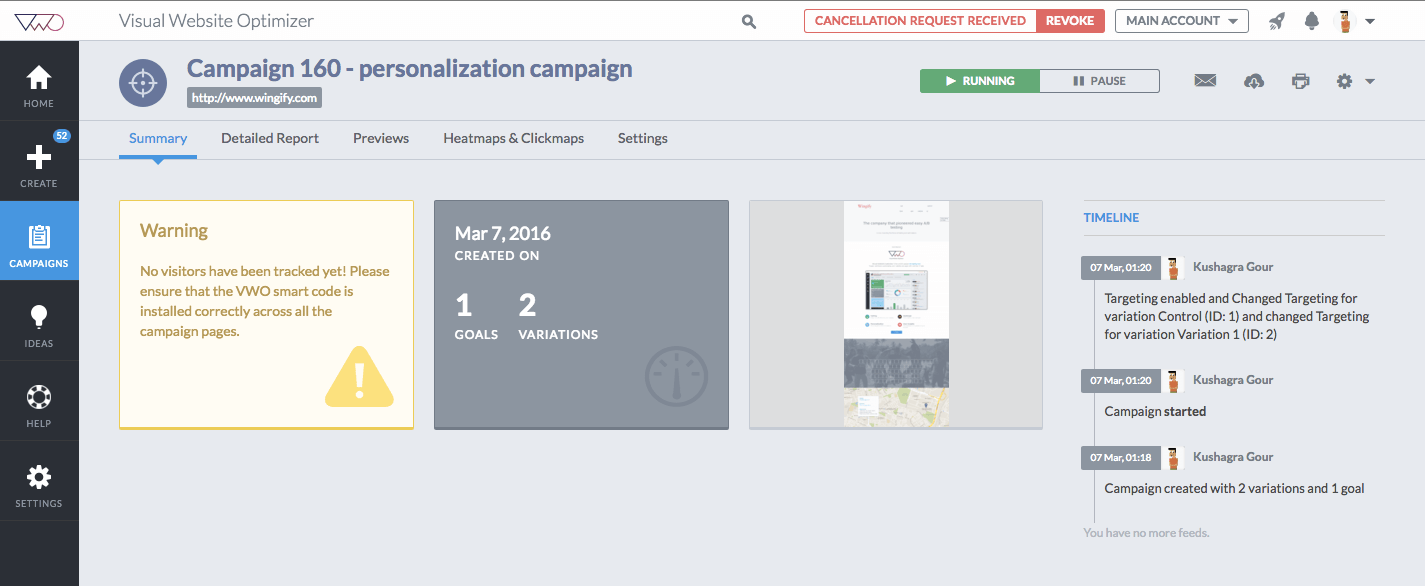
Few weeks ago, we did a redesign of our product - VWO. It wasn't a complete overhaul from scratch, but some major design decisions were…
Free objects - a generalized interpreter pattern
In the GOF book, the interpreter pattern is probably one of the most poorly described patterns. The interpreter pattern basically consists…
SuperElasticsearch - More Python goodness in elasticsearch-py
We have been using Elasticsearch for storing analytics data. This data stored in Elasticsearch is used in the Post Report Segmentation…
Wingify at Meta Refresh 2015
After hosting the Meta Refresh Delhi Runup Event, it was time for us at Wingify to prep up for MetaRefresh. We were very excited to…
Meta Refresh 2015 Delhi Run-up Event hosted at Wingify
Giving back to the community has always been a priority at Wingify, be it through open sourcing internal projects or via organizing…
Q-Directives - A Faster Directive System For Angular.js
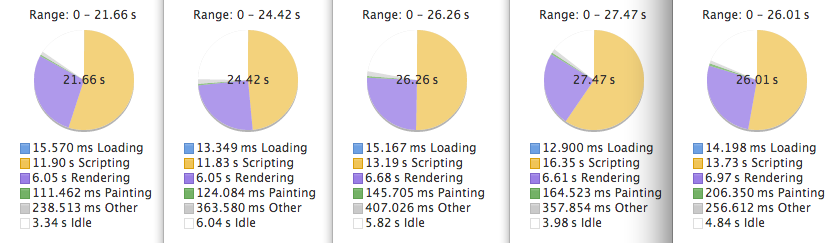
Performance matters, and an Angular.js developer would especially know it. Several watchers in a digest cycle can often be a bottleneck, and…
Elasticsearch for Analytics
Elasticsearch is essentially a distributed search-engine but there have been more than one example of companies and projects using…
Meta Refresh 2015 Delhi Run-Up Event
Meta Refresh is an event organised by HasGeek that focuses on design, user experience and the front-end web. The current iteration of Meta…
Open source at Wingify
At Wingify, we believe in open source and actively seek opportunities to give back to the community. We make use of a lot of open source…
Testing AngularJS Apps End to End Using Protractor
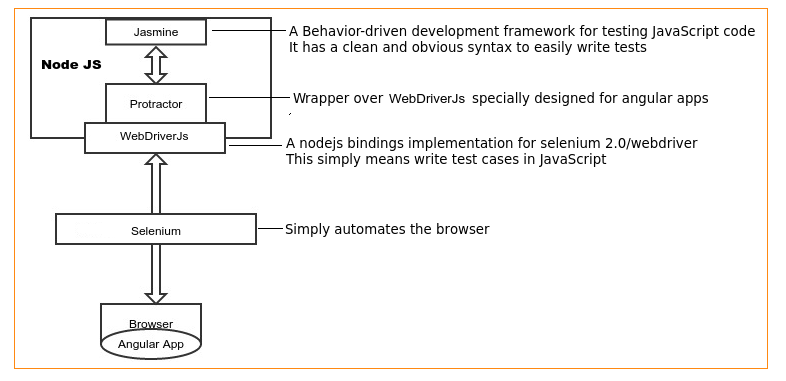
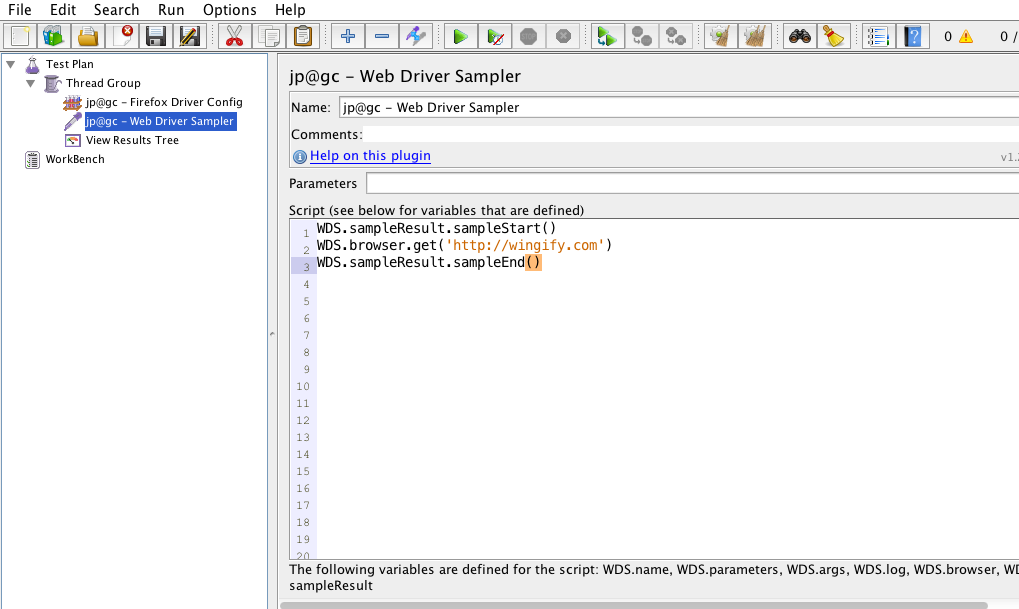
We, at Wingify, have been writing e2e test cases for our A/B testing app for the past 5 months using protractor. Writing e2e scripts is easy…
Overcoming the Challenges of Performance Testing Single-page Apps
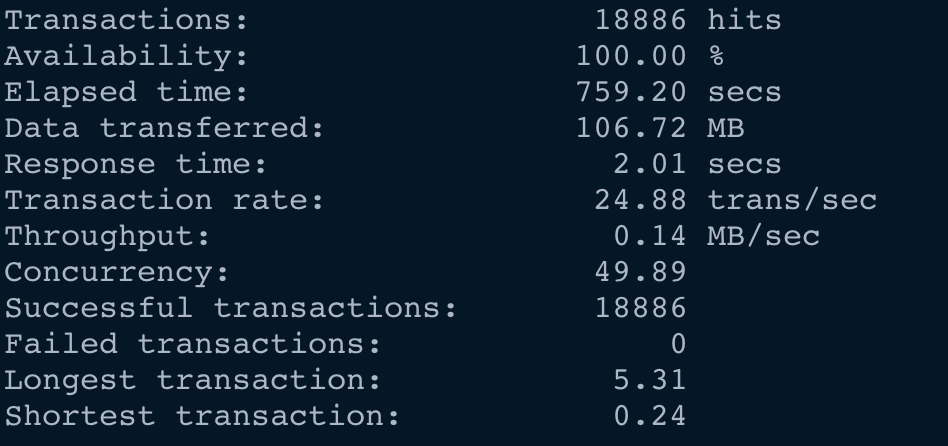
To begin with, lets talk about two of the most important things are that come to mind when we talk about performance testing. The Metrics to…
Wingify at CSSConf / JSConf Asia 2014
Back in November, I, along with some colleagues from Wingify went to Singapore to attend CSSConf and JSConf Asia. A part of DevFest Asia, it…
JSFoo Delhi Run-up Event @ Wingify
Last week, we announced that Wingify would be sponsoring the JSFoo 2014 conference in Bangalore. We have always been looking out for…
JSFoo 2014 Delhi Run-up Event + JS Contest
The front-end has become the heart of today's web application development, and JavaScript drives a core part of it. New technologies…
Open Sourcing DOM Comparator
DOM Comparator is a JavaScript library that analyzes and compares two HTML strings, and returns back a diff object. It returns an output…
Wingify at The Fifth Elephant
The Fifth Elephant is a popular conference in India around the Big Data ecosystem. It happened last week in Bangalore. And we were proud to…
Dynamic CDN
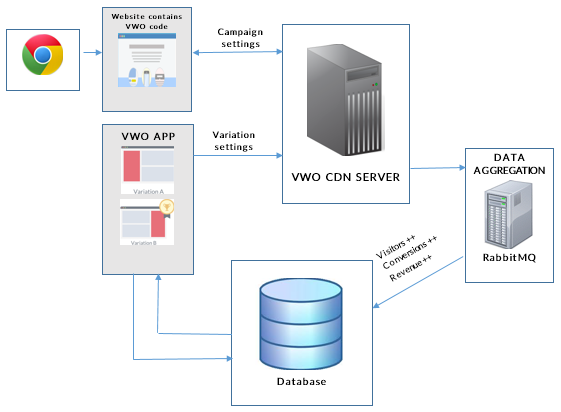
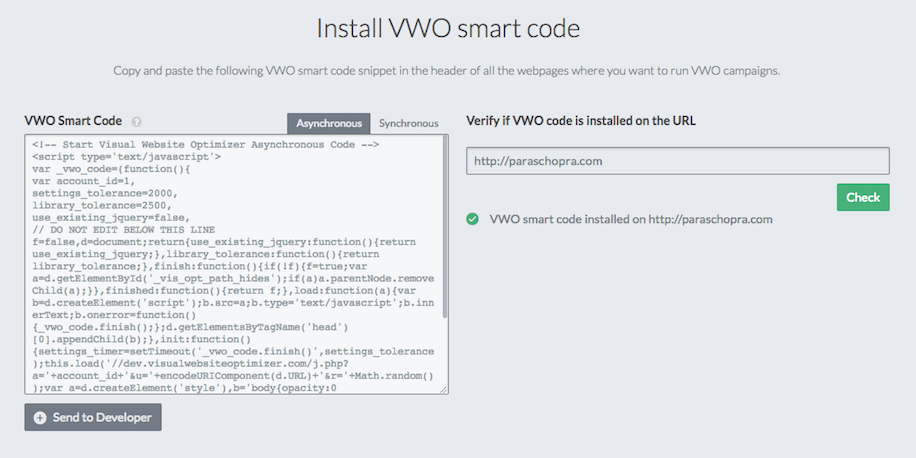
We, at Wingify, handle not just our own traffic, but also the traffic of major websites such as Microsoft, AMD, Groupon, and WWF that…
We are sponsoring The Fifth Elephant 2014
We are excited to announce our sponsorship of The Fifth Elephant - a popular conference around the Big Data ecosystem. The conference will…
Fast Storage with RocksDB
In November last year, I started developing an infrastructure that would allow us to collect, store, search and retrieve high volume data…
Automated e2e testing- WebDriverJS, Jasmine and Protractor
e2e or end-to-end or UI testing is a methodology used to test whether the flow of an application is performing as designed from start to…
Scaling with Queues
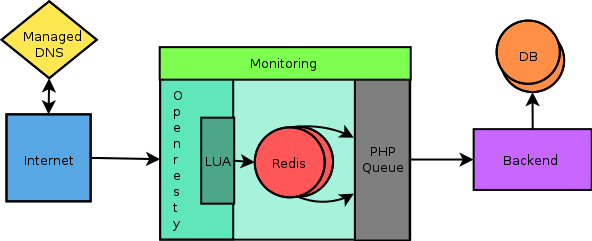
Our home-grown geo-distributed architecture based CDN allows us to delivery dynamic javascript content with minimum latencies possible…
Internship experience @Wingify
When I got an opportunity of interning with the engineering team at Wingify it made me ecstatic because of an exciting office with…
Getting 60 FPS using Chrome devtools
This post is about making your web page perform better using a real world example. As you know, we recently launched a very cool animated…
please.js - A simple PostMessage based communication library
In one of our previous posts, we talked about the problems we faced when communicating with frames on a different domain in our application…
How We Made The Animated A/B Testing Guide
Recently, we launched our first ever animated guide to A/B testing which made it to the top of HN homepage (Yay!). In this post, I'll go…
jQuery Promises: The answer to PostMessage's asynchrony
Visual Website Optimizer's editor component loads a website for editing using a proxy tunnel. It put a big restriction on what kind of…
Introduction: Engineering @ Wingify
I clearly remember the summer of 2010 when we were about to launch our product Visual Website Optimizer out of beta and almost all the…